光线在均匀介质中沿直线传播,在非均匀介质中的传播,则可利用折射定律进行解析求解,而对于较为复杂的情况,可以利用数值方法模拟求解。
具体可以将连续介质离散化,每一小块区间内的折射率近似看作不变,由起始位置开始逐步求出下一点位置,直到终点。当小区间很小时,散点之间的连线近似可看作光线的路径。
此处,对折射率一维线性变化的介质做了一次模拟,折射率仅与y方向上成线性关系。对于其他折射率一维变化的介质只需修改一下折射率函数(Nfun部分)即可,对于二维,乃至三维的情况,需要首先对全空间进行折射率的求解,其过程类似。
!========================================================================
! FileName: ConsoleApp.f90
! Author: hsyyf
! Email: 931107419@qq.com
! HomePage: http://www.hsyyf.me
! LastChange: 2012-06-13 14:35:32
!========================================================================
PROGRAM Main()
IMPLICIT NONE
INTEGER,PARAMETER :: N=1000
REAL(8) :: y(N),x(N),h,N12(N)
INTEGER :: i
OPEN(10,FILE='Data.txt')
h=0.01d0
DO i=0,N
y(i)=i*h
ENDDO
x(0)=0
CALL Nfun(N,Y,N12)
CALL Line(N,x,y,N12,h)
DO i=1,N-1
write(10,*) X(i),Y(i)
ENDDO
END PROGRAM Main
SUBROUTINE Line(N,x,y,N12,h)
REAL(8) :: x(N),y(N),N12(N),h,N1
REAL(8) :: pi,delta1,delta2
INTEGER :: i
x(0)=0.d0
pi=3.1415926d0
delta1=pi/3.d0
DO i=1,N
N1=N12(i)/N12(i-1)
delta2=asin(sin(delta1)/N1)
x(i)=x(i-1)+h*tan(delta2)
delta1=delta2
ENDDO
END
SUBROUTINE Nfun(N,Y,N12)
REAL(8) :: Y(N),N12(N)
INTEGER :: N,i
DO i=0,N
N12(i)=1+y(i)
ENDDO
END
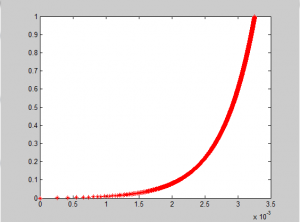
运行结果如图所示,可见,单纯的线性关系,最后导致的结果将使得光线有一个较大的偏折:
学光学的感觉好亲切啊,虽然什么都看不懂……
从现在开始准备下次考试。。。到底是考四级还是六级呢
???